@@ -3,12 +3,13 @@ title: 二分查找
33date : 2023-02-09
44tags :
55 - binary-search
6+ - algorithms
67categories : algorithms
78---
89
910![ ] ( https://img.starfish.ink/algorithm/binary-search-banner.png )
1011
11- > 二分查找【折半查找】,一种简单高效的搜索算法,一般是利用有序数组的特性,通过逐步比较中间元素来快速定位目标值
12+ > 二分查找【折半查找】,一种简单高效的搜索算法,一般是利用有序数组的特性,通过逐步比较中间元素来快速定位目标值。
1213>
1314> 二分查找并不简单,Knuth 大佬(发明 KMP 算法的那位)都说二分查找:** 思路很简单,细节是魔鬼** 。比如二分查找让人头疼的细节问题,到底要给 ` mid ` 加一还是减一,while 里到底用 ` <= ` 还是 ` < ` 。
1415
@@ -68,7 +69,7 @@ int binarySearch(int[] nums, int target) {
6869- 二分查找针对的是有序数组
6970- 数据量太小太大都不是很适用二分(太小直接顺序遍历就够了,太大的话对连续内存空间要求更高)
7071
71- ### [ 704. 二分查找] ( https://leetcode.cn/problems/binary-search/ ) (基本的二分搜索)
72+ ### [ 二分查找『704』 ] ( https://leetcode.cn/problems/binary-search/ ) (基本的二分搜索)
7273
7374> 给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。
7475>
@@ -95,6 +96,10 @@ int binarySearch(int[] nums, int target) {
9596
9697答:因为初始化 ` right ` 的赋值是 ` nums.length - 1 ` ,即最后一个元素的索引,而不是 ` nums.length ` 。
9798
99+ 这二者可能出现在不同功能的二分查找中,区别是:前者相当于两端都闭区间 ` [left, right] ` ,后者相当于左闭右开区间 ` [left, right) ` 。因为索引大小为 ` nums.length ` 是越界的,所以我们把 ` right ` 这一边视为开区间。
100+
101+ 我们这个算法中使用的是前者 ` [left, right] ` 两端都闭的区间。** 这个区间其实就是每次进行搜索的区间** 。
102+
98103** 2、为什么 ` left = mid + 1 ` ,` right = mid - 1 ` ?我看有的代码是 ` right = mid ` 或者 ` left = mid ` ,没有这些加加减减,到底怎么回事,怎么判断** ?
99104
100105答:这也是二分查找的一个难点,不过只要你能理解前面的内容,就能够很容易判断。
@@ -103,7 +108,22 @@ int binarySearch(int[] nums, int target) {
103108
104109当然是去搜索区间 ` [left, mid-1] ` 或者区间 ` [mid+1, right] ` 对不对?** 因为 ` mid ` 已经搜索过,应该从搜索区间中去除** 。
105110
106-
111+ > ##### 1. ** 左闭右闭区间 ` [left, right] ` **
112+ >
113+ > - ** 循环条件** :` while (left <= right) ` ,因为 ` left == right ` 时区间仍有意义。
114+ > - 边界调整:
115+ > - ` nums[mid] < target ` → ` left = mid + 1 ` (排除 ` mid ` 左侧)
116+ > - ` nums[mid] > target ` → ` right = mid - 1 ` (排除 ` mid ` 右侧)
117+ > - 适用场景:明确目标值存在于数组时,直接返回下标。
118+ >
119+ > ##### 2. ** 左闭右开区间 ` [left, right) ` **
120+ >
121+ > - ** 初始化** :` right = nums.length ` 。
122+ > - ** 循环条件** :` while (left < right) ` ,因为 ` left == right ` 时区间为空。
123+ > - 边界调整:
124+ > - ` nums[mid] < target ` → ` left = mid + 1 `
125+ > - ` nums[mid] > target ` → ` right = mid ` (右开,不包含 ` mid ` )
126+ > - ** 适用场景** :需要处理目标值可能不在数组中的情况,例如插入位置问题
107127
108128> 比如说给你有序数组 ` nums = [1,2,2,2,3] ` ,` target ` 为 2,此算法返回的索引是 2,没错。但是如果我想得到 ` target ` 的左侧边界,即索引 1,或者我想得到 ` target ` 的右侧边界,即索引 3,这样的话此算法是无法处理的。
109129>
@@ -112,7 +132,7 @@ int binarySearch(int[] nums, int target) {
112132### 寻找左侧边界的二分搜索
113133
114134``` java
115- public static int leftBound(int [] nums, int target) {
135+ public int leftBound(int [] nums, int target) {
116136 int left = 0 ;
117137 int right = nums. length - 1 ;
118138 while (left <= right) {
@@ -122,7 +142,7 @@ public static int leftBound(int[] nums, int target) {
122142 } else if (nums[mid] < target) {
123143 left = mid + 1 ;
124144 } else {
125- // mid 是第一个元素,或者前一个元素不等于查找值,锁定
145+ // mid 是第一个元素,或者前一个元素不等于查找值,锁定,且返回的是mid
126146 if (mid == 0 || nums[mid - 1 ] != target) return mid;
127147 else right = mid - 1 ;
128148 }
@@ -134,7 +154,7 @@ public static int leftBound(int[] nums, int target) {
134154### 寻找右侧边界的二分查找
135155
136156``` java
137- public static int rightBound(int [] nums, int target){
157+ public int rightBound(int [] nums, int target){
138158 int left = 0 ;
139159 int right = nums. length - 1 ;
140160 while (left <= right){
@@ -174,99 +194,7 @@ public int firstNum(int[] nums, int target) {
174194
175195
176196
177- ### [ 153. 寻找旋转排序数组中的最小值] ( https://leetcode-cn.com/problems/find-minimum-in-rotated-sorted-array/ )
178-
179- > 已知一个长度为 n 的数组,预先按照升序排列,经由 1 到 n 次 旋转 后,得到输入数组。例如,原数组 nums = [ 0,1,2,4,5,6,7] 在变化后可能得到:
180- > 若旋转 4 次,则可以得到 [ 4,5,6,7,0,1,2] 若旋转 7 次,则可以得到 [ 0,1,2,4,5,6,7]
181- > 注意,数组 [ a[ 0] , a[ 1] , a[ 2] , ..., a[ n-1]] 旋转一次 的结果为数组 [ a[ n-1] , a[ 0] , a[ 1] , a[ 2] , ..., a[ n-2]] 。
182- >
183- > 给你一个元素值 互不相同 的数组 nums ,它原来是一个升序排列的数组,并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。
184- >
185- > 你必须设计一个时间复杂度为 $O(log n)$ 的算法解决此问题。
186- >
187- > ```
188- > 输入:nums = [3,4,5,1,2]
189- > 输出:1
190- > 解释:原数组为 [1,2,3,4,5] ,旋转 3 次得到输入数组。
191- > ```
192- >
193- >```
194- > 输入:nums = [11,13,15,17]
195- > 输出:11
196- > 解释:原数组为 [11,13,15,17] ,旋转 4 次得到输入数组。
197- > ```
198-
199- **思路**:
200-
201- 升序数组+旋转,仍然是部分有序,考虑用二分查找。
202-
203- 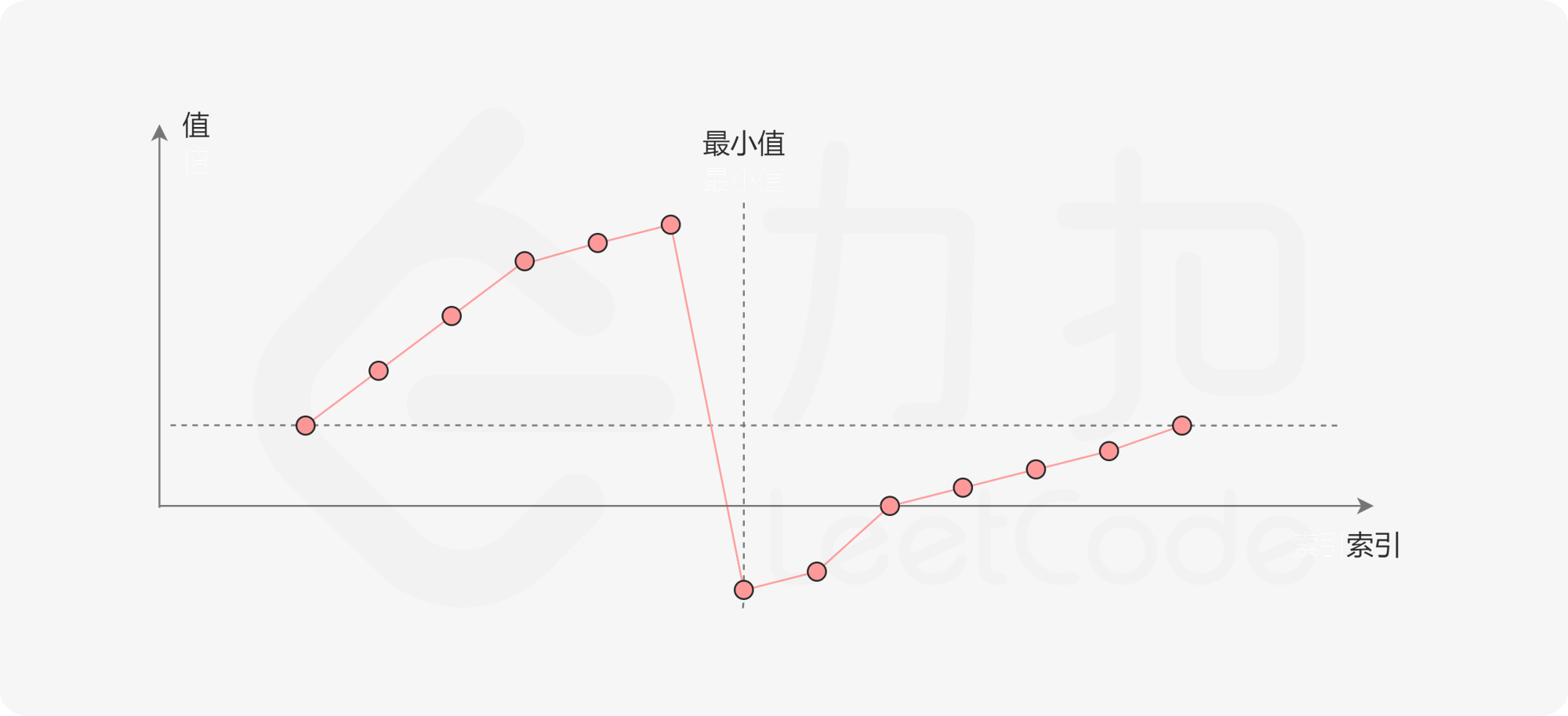
204-
205- > 我们先搞清楚题目中的数组是通过怎样的变化得来的,基本上就是等于将整个数组向右平移
206-
207- > 这种二分查找难就难在,arr[mid] 跟谁比。
208- >
209- > 我们的目的是:当进行一次比较时,一定能够确定答案在 mid 的某一侧。一次比较为 arr[mid] 跟谁比的问题。
210- > 一般的比较原则有:
211- >
212- > - 如果有目标值 target,那么直接让 arr[mid] 和 target 比较即可。
213- > - 如果没有目标值,一般可以考虑 **端点**
214- >
215- > 如果中值 < 右值,则最小值在左半边,可以收缩右边界。
216- > 如果中值 > 右值,则最小值在右半边,可以收缩左边界。
217-
218- 旋转数组,最小值右侧的元素肯定都小于或等于数组中的最后一个元素 `nums[n-1]`,左侧元素都大于 `num[n-1]`
219-
220- ```java
221- public static int findMin(int[] nums) {
222- int left = 0;
223- int right = nums.length - 1;
224- //左闭右开
225- while (left < right) {
226- int mid = left + (right - left) / 2;
227- //疑问:为什么right = mid;而不是 right = mid-1;
228- //解答:{4,5,1,2,3},如果right = mid-1,则丢失了最小值1
229- if (nums[mid] < nums[right]) {
230- right = mid;
231- } else {
232- left = mid + 1;
233- }
234- }
235- //循环结束条件,left = right,最小值输出nums[left]或nums[right]均可
236- return nums[left];
237- }
238- ```
239-
240- ** 如果是求旋转数组中的最大值呢**
241-
242- ``` java
243- public static int findMax(int [] nums) {
244- int left = 0 ;
245- int right = nums. length - 1 ;
246-
247- while (left < right) {
248- int mid = left + (right - left) >> 1 ;
249-
250- // 因为向下取整,left可能会等于mid,所以要考虑
251- if (nums[left] < nums[right]) {
252- return nums[right];
253- }
254-
255- // [left,mid] 是递增的,最大值只会在[mid,right]中
256- if (nums[left] < nums[mid]) {
257- left = mid;
258- } else {
259- // [mid,right]递增,最大值只会在[left, mid-1]中
260- right = mid - 1 ;
261- }
262- }
263- return nums[left];
264- }
265- ```
266-
267-
268-
269- ### [ 33. 搜索旋转排序数组] ( https://leetcode-cn.com/problems/search-in-rotated-sorted-array/ )
197+ ### [ 搜索旋转排序数组『33』] ( https://leetcode-cn.com/problems/search-in-rotated-sorted-array/ )
270198
271199> 整数数组 nums 按升序排列,数组中的值 互不相同 。
272200>
@@ -297,14 +225,14 @@ public static int findMax(int[] nums) {
297225public static int search(int[] nums,int target) {
298226 if(nums.length == 0) return -1;
299227 if(nums.length == 1) return target == nums[0] ? 0 : -1;
300- int left = 0;
301- int right = nums.length - 1;
228+ int left = 0, right = nums.length - 1;
302229 while(left <= right){
303230 int mid = left + (right - left)/2;
304231 if(target == nums[mid]) return mid;
232+
305233 //左侧有序,注意是小于等于,处理最后只剩两个数的时候
306- if(nums[left] <= nums[mid]){
307- if(nums[left] <= target && target < nums[mid]){
234+ if(nums[left] <= nums[mid]){ // 左半部分 [left..mid] 有序
235+ if(nums[left] <= target && target < nums[mid]){ // target 在左半部分
308236 right = mid - 1;
309237 }else{
310238 left = mid + 1;
@@ -316,15 +244,14 @@ public static int search(int[] nums,int target) {
316244 right = mid - 1;
317245 }
318246 }
319-
320247 }
321248 return -1;
322249 }
323250```
324251
325252
326253
327- ### [ 34. 在排序数组中查找元素的第一个和最后一个位置] ( https://leetcode-cn.com/problems/find-first-and-last-position-of-element-in-sorted-array/ )
254+ ### [ 在排序数组中查找元素的第一个和最后一个位置『34』 ] ( https://leetcode-cn.com/problems/find-first-and-last-position-of-element-in-sorted-array/ )
328255
329256> 给定一个按照升序排列的整数数组 nums,和一个目标值 target。找出给定目标值在数组中的开始位置和结束位置。
330257>
@@ -387,7 +314,97 @@ public int binarySearch(int[] nums, int target, boolean findLast) {
387314
388315
389316
390- ### [ 287. 寻找重复数] ( https://leetcode-cn.com/problems/find-the-duplicate-number/ )
317+ ### [ 寻找旋转排序数组中的最小值『153』] ( https://leetcode-cn.com/problems/find-minimum-in-rotated-sorted-array/ )
318+
319+ > 已知一个长度为 n 的数组,预先按照升序排列,经由 1 到 n 次 旋转 后,得到输入数组。例如,原数组 nums = [ 0,1,2,4,5,6,7] 在变化后可能得到:
320+ > 若旋转 4 次,则可以得到 [ 4,5,6,7,0,1,2] 若旋转 7 次,则可以得到 [ 0,1,2,4,5,6,7]
321+ > 注意,数组 [ a[ 0] , a[ 1] , a[ 2] , ..., a[ n-1]] 旋转一次 的结果为数组 [ a[ n-1] , a[ 0] , a[ 1] , a[ 2] , ..., a[ n-2]] 。
322+ >
323+ > 给你一个元素值 互不相同 的数组 nums ,它原来是一个升序排列的数组,并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。
324+ >
325+ > 你必须设计一个时间复杂度为 $O(log n)$ 的算法解决此问题。
326+ >
327+ > ```
328+ > 输入:nums = [3,4,5,1,2]
329+ > 输出:1
330+ > 解释:原数组为 [1,2,3,4,5] ,旋转 3 次得到输入数组。
331+ > ```
332+ >
333+ >```
334+ > 输入:nums = [11,13,15,17]
335+ > 输出:11
336+ > 解释:原数组为 [11,13,15,17] ,旋转 4 次得到输入数组。
337+ > ```
338+
339+ **思路**:
340+
341+ 升序数组+旋转,仍然是部分有序,考虑用二分查找。
342+
343+ 
344+
345+ > 我们先搞清楚题目中的数组是通过怎样的变化得来的,基本上就是等于将整个数组向右平移
346+
347+ > 这种二分查找难就难在,arr[mid] 跟谁比。
348+ >
349+ > 我们的目的是:当进行一次比较时,一定能够确定答案在 mid 的某一侧。一次比较为 arr[mid] 跟谁比的问题。
350+ > 一般的比较原则有:
351+ >
352+ > - 如果有目标值 target,那么直接让 arr[mid] 和 target 比较即可。
353+ > - 如果没有目标值,一般可以考虑 **端点**
354+ >
355+ > 如果中值 < 右值,则最小值在左半边,可以收缩右边界。
356+ > 如果中值 > 右值,则最小值在右半边,可以收缩左边界。
357+
358+ 旋转数组,最小值右侧的元素肯定都小于或等于数组中的最后一个元素 `nums[n-1]`,左侧元素都大于 `num[n-1]`
359+
360+ ```java
361+ public static int findMin(int[] nums) {
362+ int left = 0;
363+ int right = nums.length - 1;
364+ //左闭右开
365+ while (left < right) {
366+ int mid = left + (right - left) / 2;
367+ //疑问:为什么right = mid;而不是 right = mid-1;
368+ //解答:{4,5,1,2,3},如果right = mid-1,则丢失了最小值1
369+ if (nums[mid] < nums[right]) {
370+ right = mid;
371+ } else {
372+ left = mid + 1;
373+ }
374+ }
375+ //循环结束条件,left = right,最小值输出nums[left]或nums[right]均可
376+ return nums[left];
377+ }
378+ ```
379+
380+ ** 如果是求旋转数组中的最大值呢**
381+
382+ ``` java
383+ public static int findMax(int [] nums) {
384+ int left = 0 ;
385+ int right = nums. length - 1 ;
386+
387+ while (left < right) {
388+ int mid = left + (right - left) >> 1 ;
389+
390+ // 因为向下取整,left可能会等于mid,所以要考虑
391+ if (nums[left] < nums[right]) {
392+ return nums[right];
393+ }
394+
395+ // [left,mid] 是递增的,最大值只会在[mid,right]中
396+ if (nums[left] < nums[mid]) {
397+ left = mid;
398+ } else {
399+ // [mid,right]递增,最大值只会在[left, mid-1]中
400+ right = mid - 1 ;
401+ }
402+ }
403+ return nums[left];
404+ }
405+ ```
406+
407+ ### [ 寻找重复数『287』] ( https://leetcode-cn.com/problems/find-the-duplicate-number/ )
391408
392409> 给定一个包含 n + 1 个整数的数组 nums ,其数字都在 [ 1, n] 范围内(包括 1 和 n),可知至少存在一个重复的整数。
393410>
@@ -446,7 +463,7 @@ public int findDuplicate(int[] nums) {
446463
447464
448465
449- ### [ 162. 寻找峰值] ( https://leetcode-cn.com/problems/find-peak-element/ )
466+ ### [ 寻找峰值『162』 ] ( https://leetcode-cn.com/problems/find-peak-element/ )
450467
451468> 峰值元素是指其值严格大于左右相邻值的元素。
452469>
@@ -511,7 +528,7 @@ public int findPeakElement(int[] nums) {
511528
512529
513530
514- ### [ 240. 搜索二维矩阵 II] ( https://leetcode-cn.com/problems/search-a-2d-matrix-ii/ )
531+ ### [ 搜索二维矩阵 II『240』 ] ( https://leetcode-cn.com/problems/search-a-2d-matrix-ii/ )
515532
516533> [ 剑指 Offer 04. 二维数组中的查找] ( https://leetcode-cn.com/problems/er-wei-shu-zu-zhong-de-cha-zhao-lcof/ ) 一样的题目
517534>
@@ -555,7 +572,7 @@ public int findPeakElement(int[] nums) {
555572
556573
557574
558- ### [ 35. 搜索插入位置] ( https://leetcode.cn/problems/search-insert-position/ )
575+ ### [ 搜索插入位置『35』 ] ( https://leetcode.cn/problems/search-insert-position/ )
559576
560577> 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。请必须使用时间复杂度为 ` O(log n) ` 的算法。
561578>
@@ -588,7 +605,7 @@ public int searchInsert(int[] nums, int target) {
588605
589606
590607
591- ### [ 300. 最长递增子序列] ( https://leetcode.cn/problems/longest-increasing-subsequence/ )
608+ ### [ 最长递增子序列『300』 ] ( https://leetcode.cn/problems/longest-increasing-subsequence/ )
592609
593610> 给你一个整数数组 ` nums ` ,找到其中最长严格递增子序列的长度。
594611>
@@ -606,7 +623,7 @@ public int searchInsert(int[] nums, int target) {
606623
607624
608625
609- ### [4. 寻找两个正序数组的中位数](https://leetcode.cn/problems/median-of-two-sorted-arrays/)
626+ ### [寻找两个正序数组的中位数『4』 ](https://leetcode.cn/problems/median-of-two-sorted-arrays/)
610627
611628> 给定两个大小分别为 `m` 和 `n` 的正序(从小到大)数组 `nums1` 和 `nums2`。请你找出并返回这两个正序数组的 **中位数** 。
612629>
0 commit comments