|
16 | 16 |
|
17 | 17 | 通俗来讲,集合就是将一组事物组合在一起。你可以将力扣的题库看作一个集合: |
18 | 18 |
|
19 | | - |
| 19 | + |
20 | 20 |
|
21 | 21 |
|
22 | 22 |
|
23 | 23 | 也可以将力扣商店里的礼品看作一个集合: |
24 | 24 |
|
25 | | - |
| 25 | + |
26 | 26 |
|
27 | 27 | 甚至可以将桌面上的物品当作一个集合。 |
28 | 28 |
|
|
42 | 42 |
|
43 | 43 | 列表的概念是在集合的特征上形成的,它具有顺序,且长度是可变的。你可以把它看作一张购物清单: |
44 | 44 |
|
45 | | - |
| 45 | + |
46 | 46 |
|
47 | 47 | 在这张清单中: |
48 | 48 |
|
|
63 | 63 |
|
64 | 64 | 首先,数组会用一些名为 `索引` 的数字来标识每项数据在数组中的位置,且在大多数编程语言中,索引是从 `0` 算起的。我们可以根据数组中的索引,快速访问数组中的元素。 |
65 | 65 |
|
66 | | -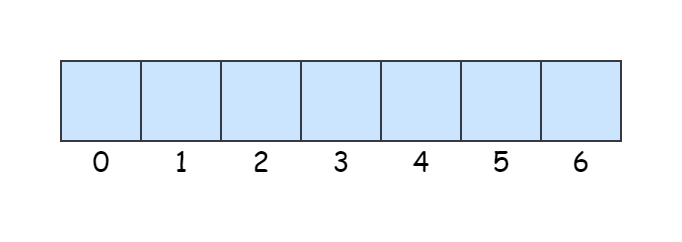 |
| 66 | + |
67 | 67 |
|
68 | 68 | **而列表中没有索引,这是数组与列表最大的不同点**。 |
69 | 69 |
|
70 | 70 | 其次,数组中的元素在内存中是连续存储的,且每个元素占用相同大小的内存。 |
71 | 71 |
|
72 | | - |
73 | | - |
74 | | -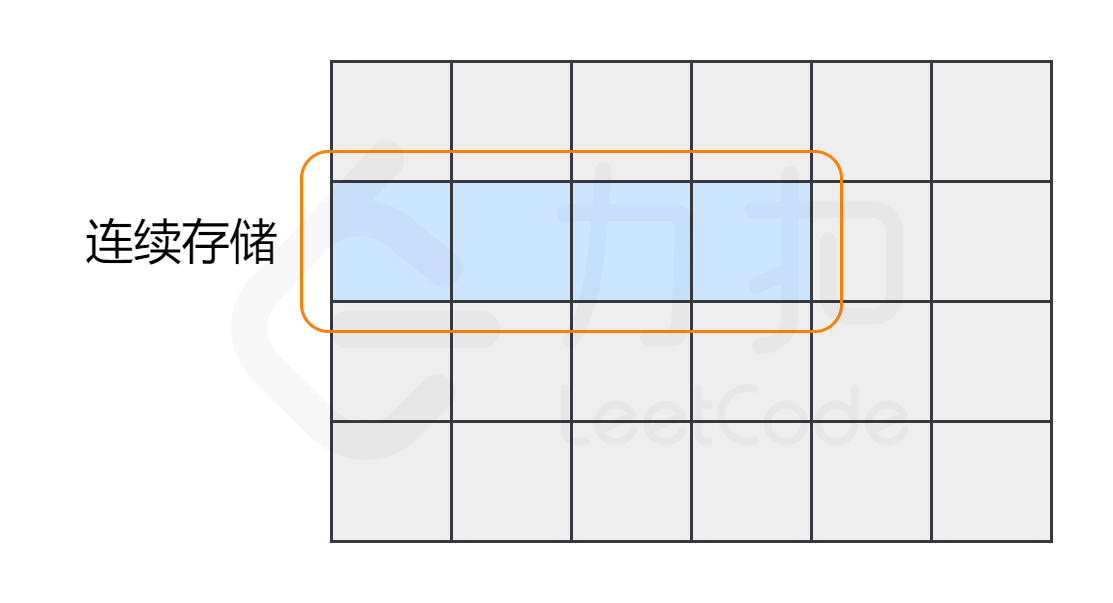 |
75 | | - |
76 | | - |
| 72 | + |
77 | 73 |
|
78 | 74 | 相反,列表中的元素在内存中可能彼此相邻,也可能不相邻。比如列表的另一种实现方式——链表,它的元素在内存中则不一定是连续的。 |
79 | 75 |
|
|
89 | 85 |
|
90 | 86 | 可以形象地将计算机中的内存看作一系列排列好的格子,这些格子中,每一个格子对应一个内存地址,数据会存储在不同的格子中。 |
91 | 87 |
|
92 | | -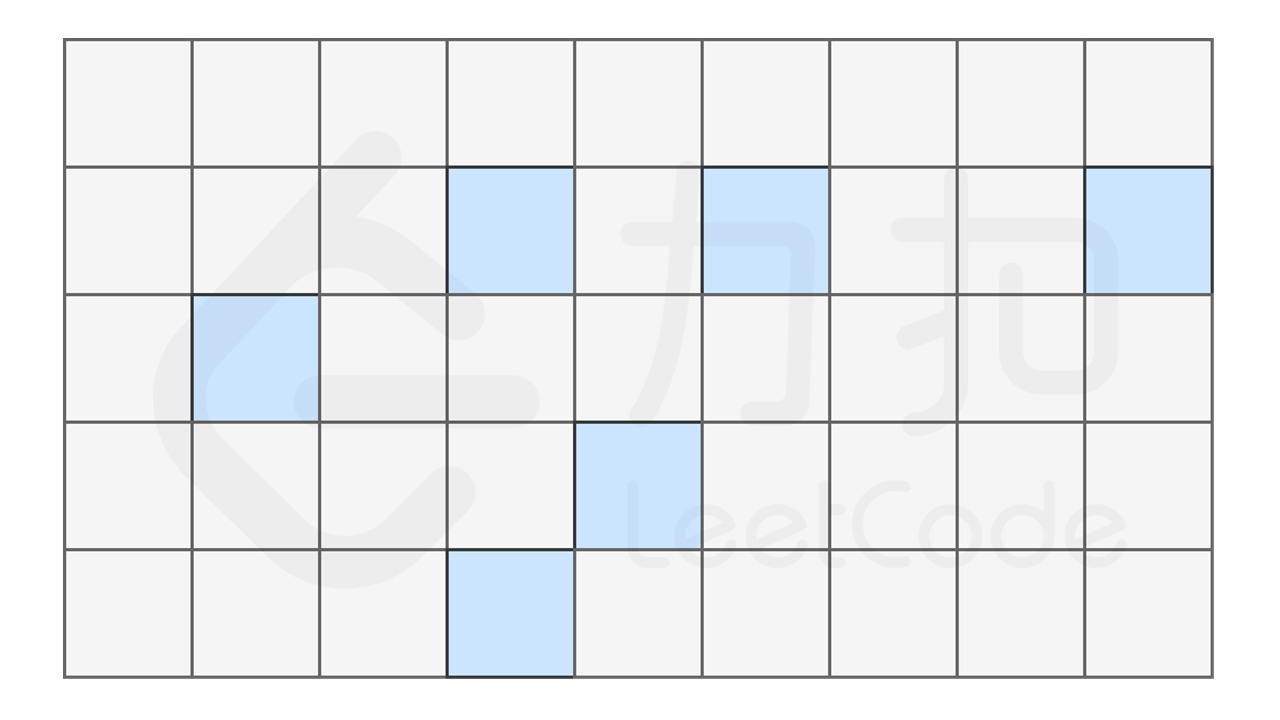 |
| 88 | + |
93 | 89 |
|
94 | 90 | 而对于数组,计算机会在内存中申请一段 **连续** 的空间,并且会记下索引为 `0` 处的内存地址。例如对于一个数组 `['oranges', 'apples', 'bananas', 'pears', 'tomatoes']`,为了方便起见,我们假设每个元素只占用一个字节,它的索引与内存地址的关系如下图所示。 |
95 | 91 |
|
96 | | -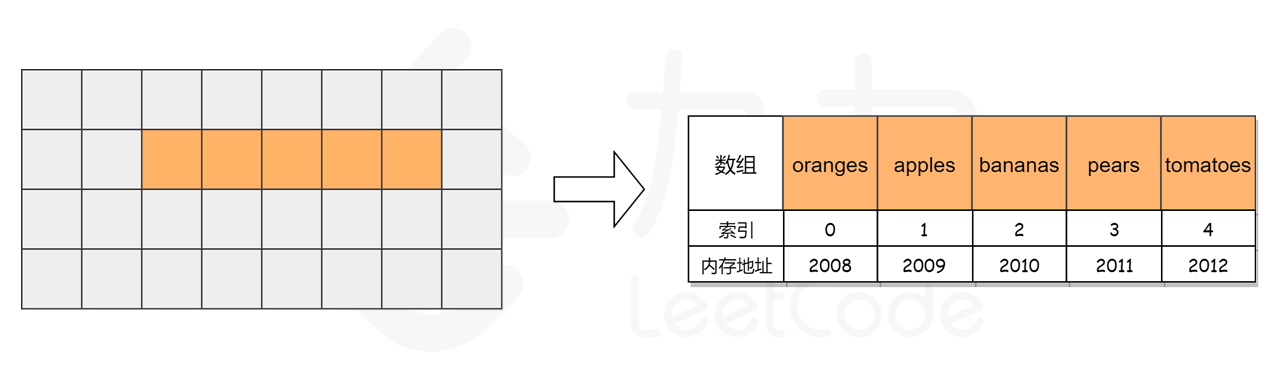 |
| 92 | + |
97 | 93 |
|
98 | 94 | 当我们访问数组中索引为 `3` 处的元素时,计算机会进行如下计算: |
99 | 95 |
|
|
110 | 106 |
|
111 | 107 | 还是上面的例子,如果我们要查找数组中是否包含元素 `pears`,计算机会从索引 `0` 开始,逐个比较对应的元素,直到找到该元素后停止搜索,或到达数组的末尾后停止。 |
112 | 108 |
|
113 | | -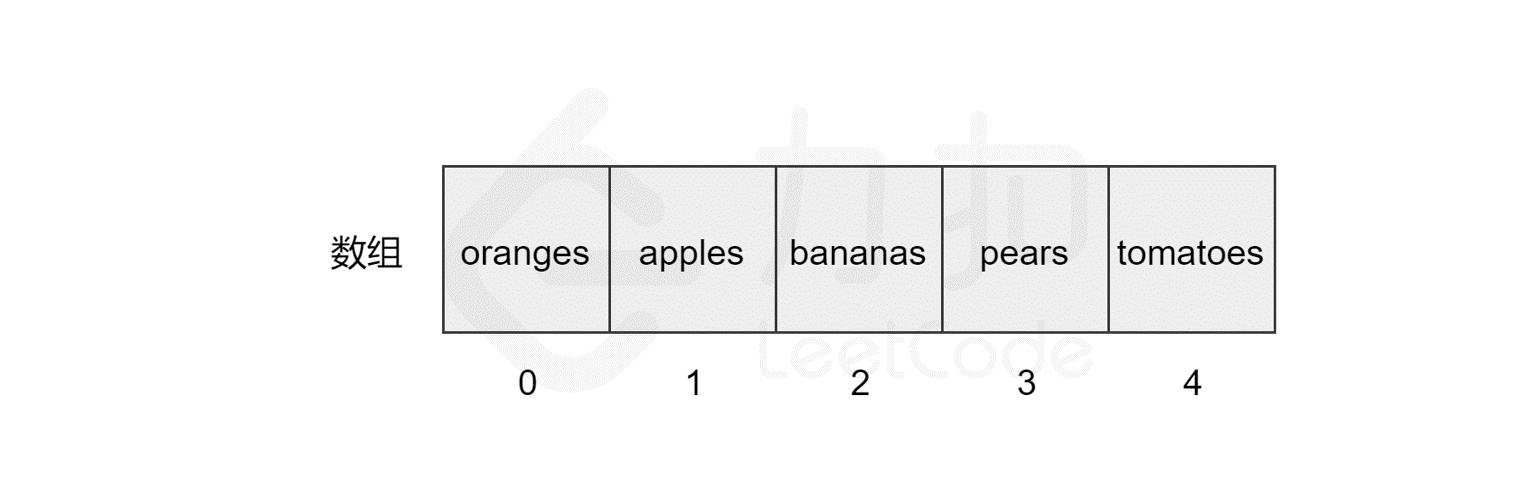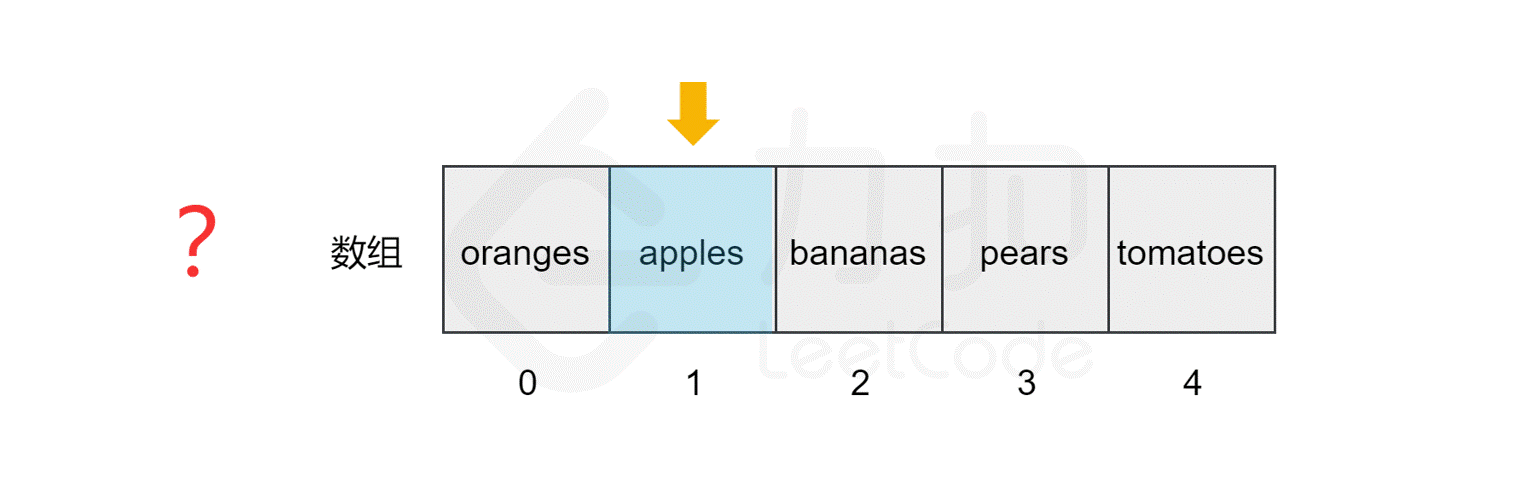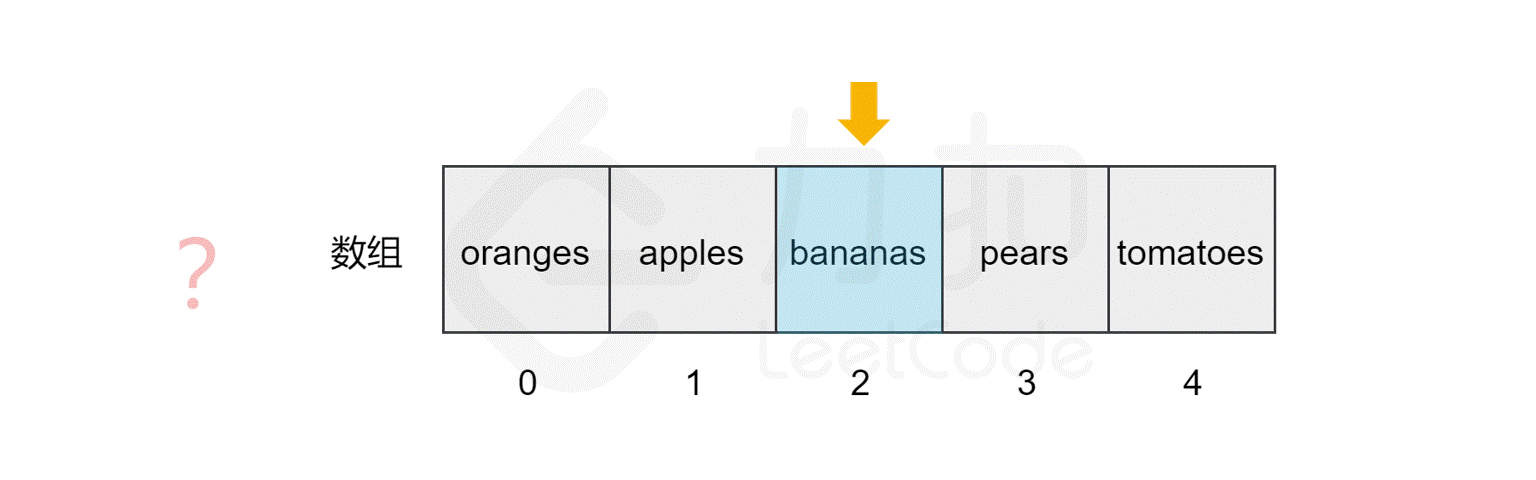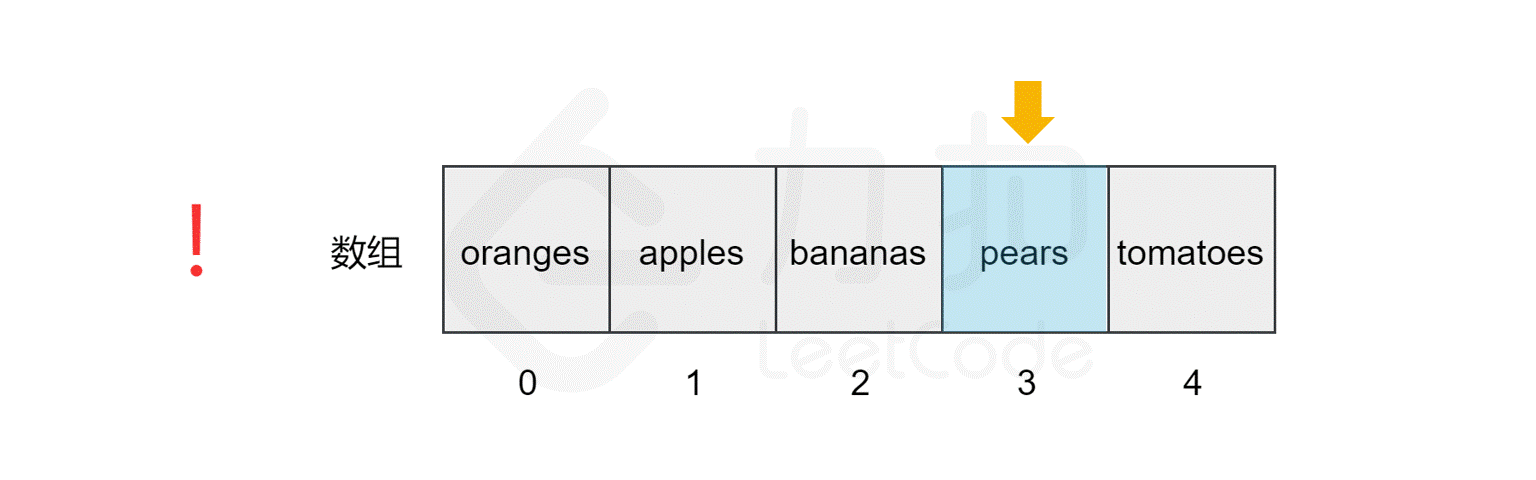 |
| 109 | + |
114 | 110 |
|
115 | 111 | 我们发现,该数组的长度为 `5`,最坏情况下(比如我们查找元素 `tomatoes` 或查找数组中不包含的元素),我们需要查询数组中的每个元素,因此时间复杂度为$ O(N)$,*N* 为数组的长度。 |
116 | 112 |
|
|
122 | 118 |
|
123 | 119 | 如果要将该元素插入到数组的末尾,只需要一步。即计算机通过数组的长度和位置计算出即将插入元素的内存地址,然后将该元素插入到指定位置即可。 |
124 | 120 |
|
125 | | -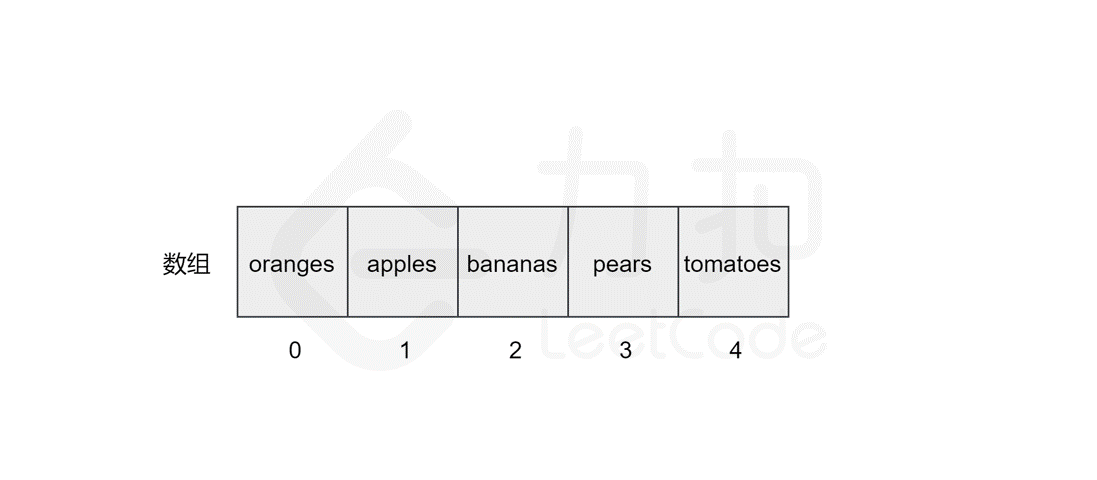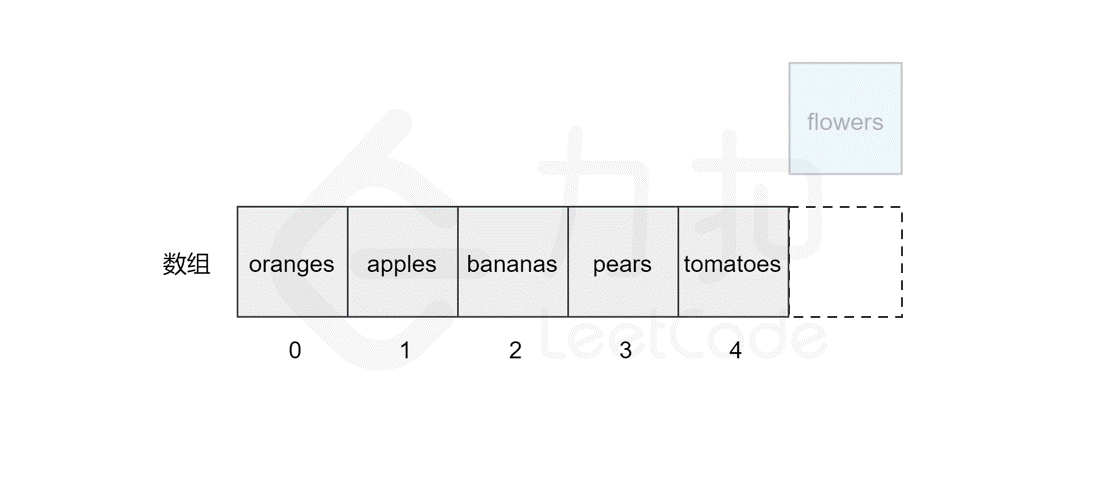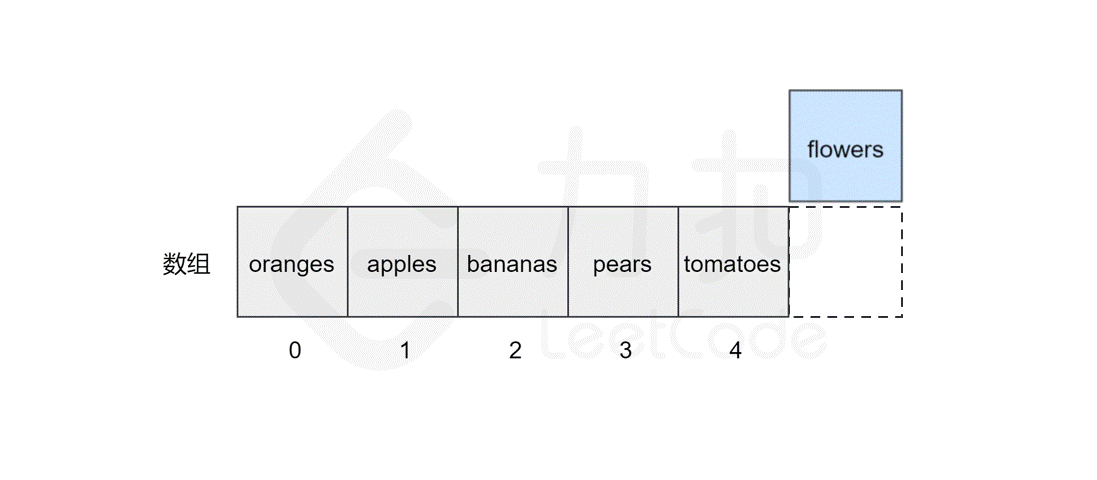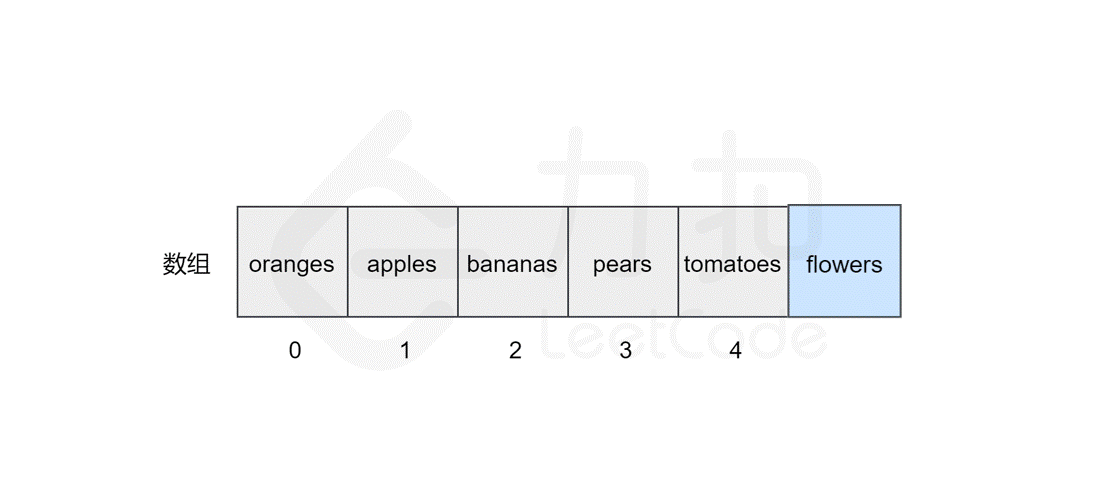 |
| 121 | + |
126 | 122 |
|
127 | 123 | 然而,如果要将该元素插入到数组中的其他位置,则会有所区别,这时我们首先需要为该元素所要插入的位置`腾出` 空间,然后进行插入操作。比如,我们想要在索引 `2` 处插入 `flowers`。 |
128 | 124 |
|
129 | | -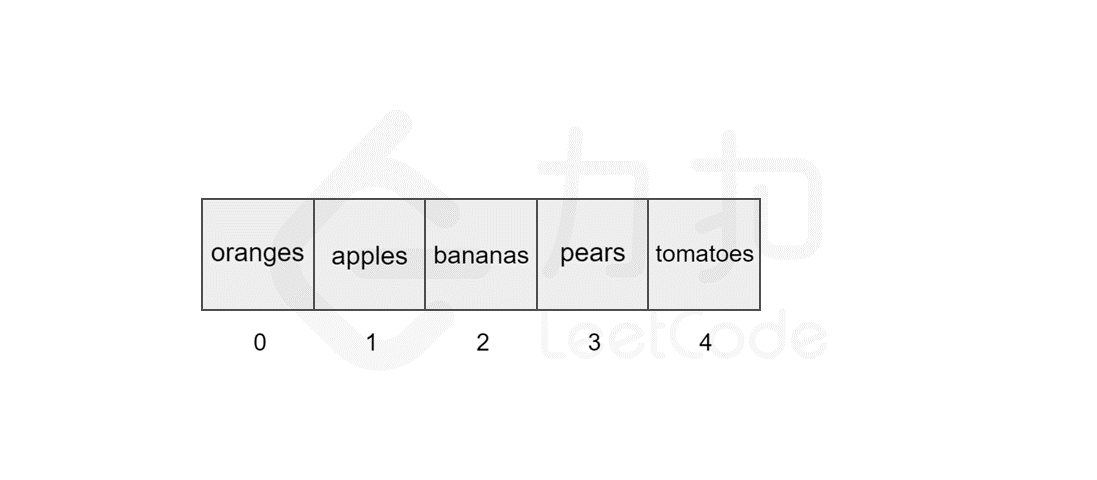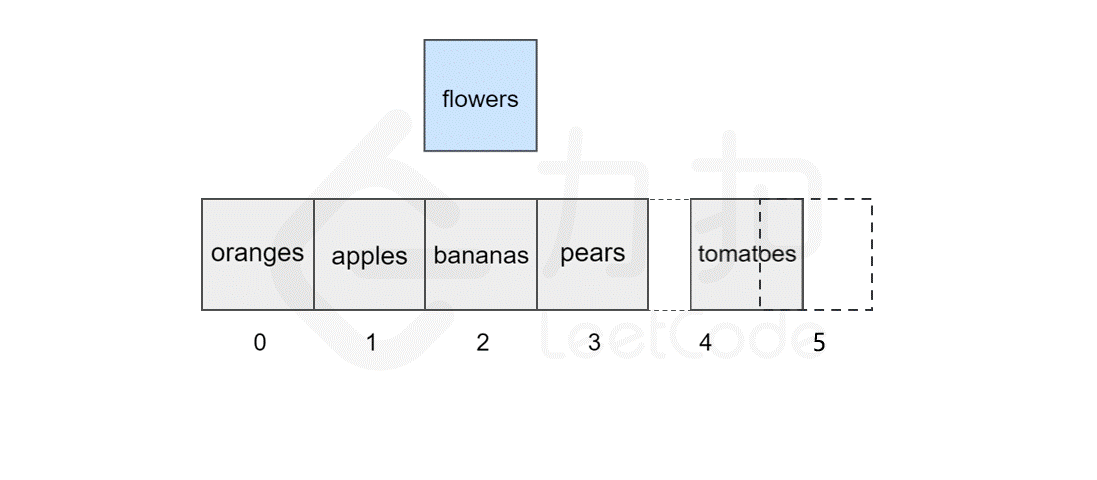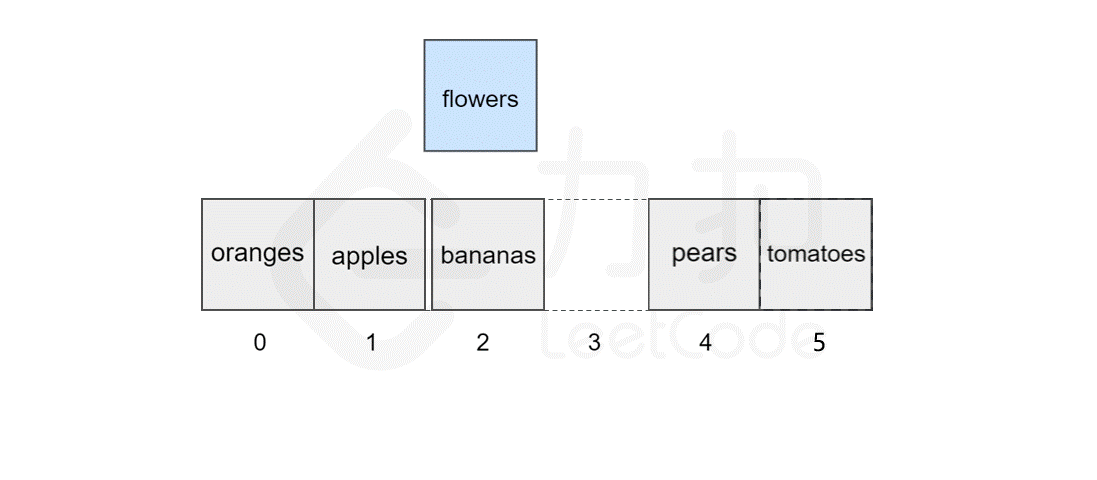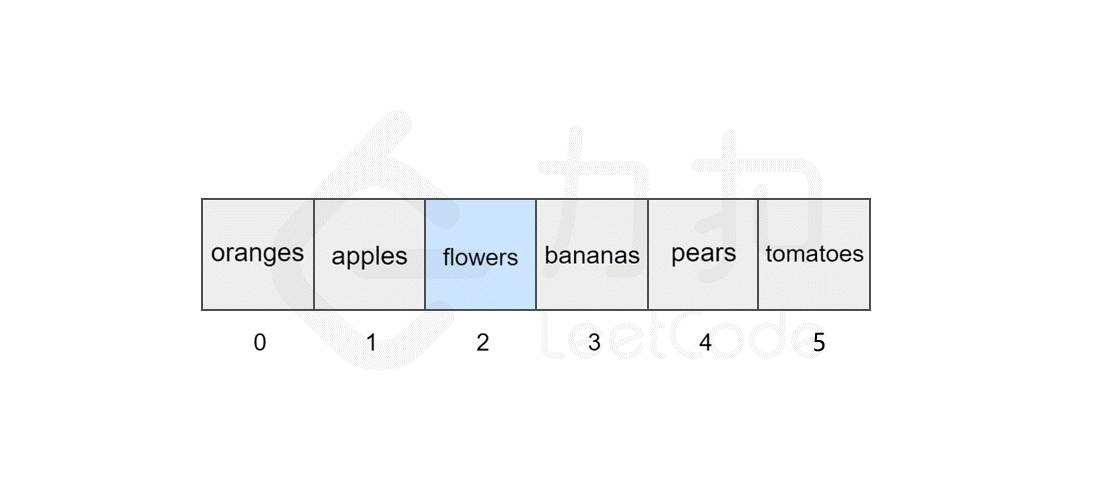 |
| 125 | + |
130 | 126 |
|
131 | 127 | 我们发现,如果需要频繁地对数组元素进行插入操作,会造成时间的浪费。事实上,另一种数据结构,即链表可以有效解决这个问题。 |
132 | 128 |
|
|
138 | 134 |
|
139 | 135 | 以删除索引 `1` 中的元素 `apples` 为例,具体过程如图所示。 |
140 | 136 |
|
141 | | -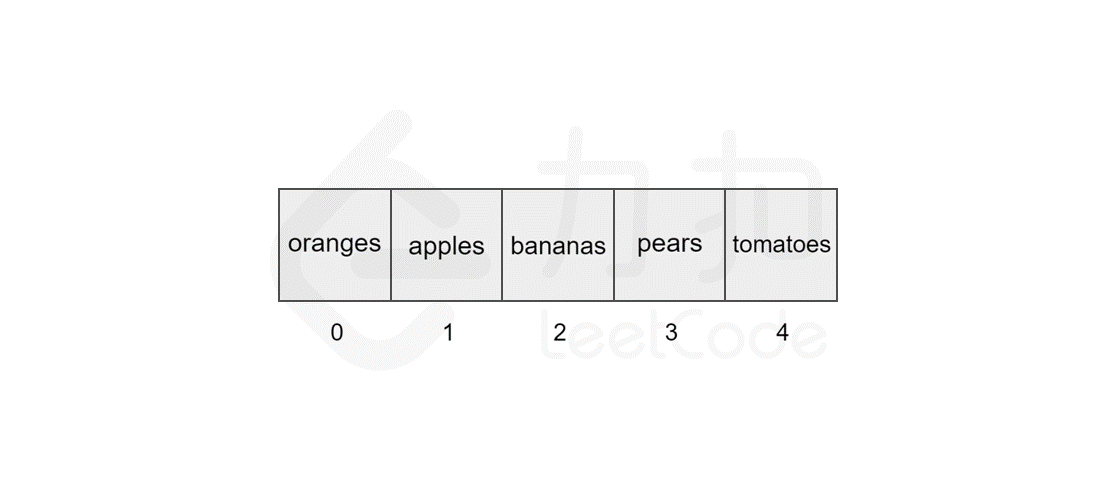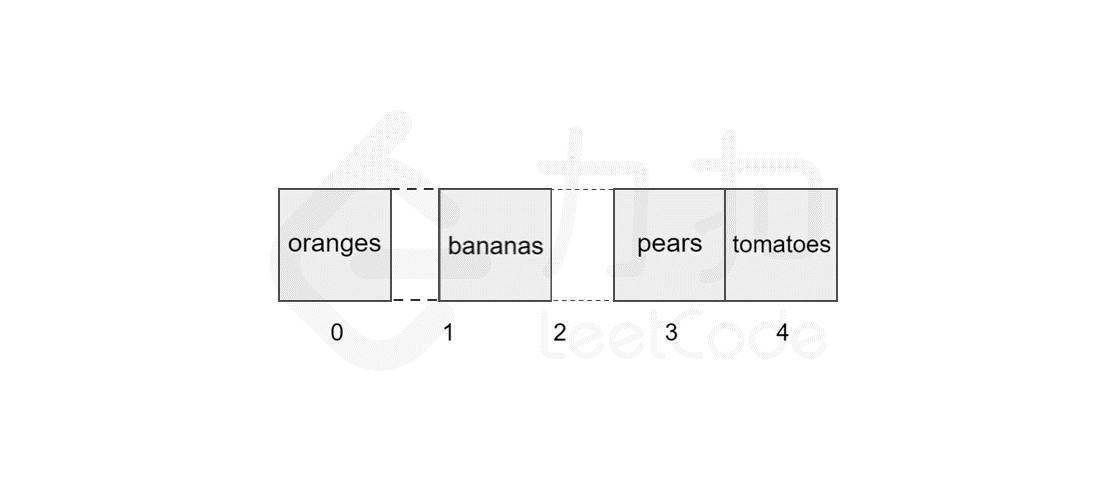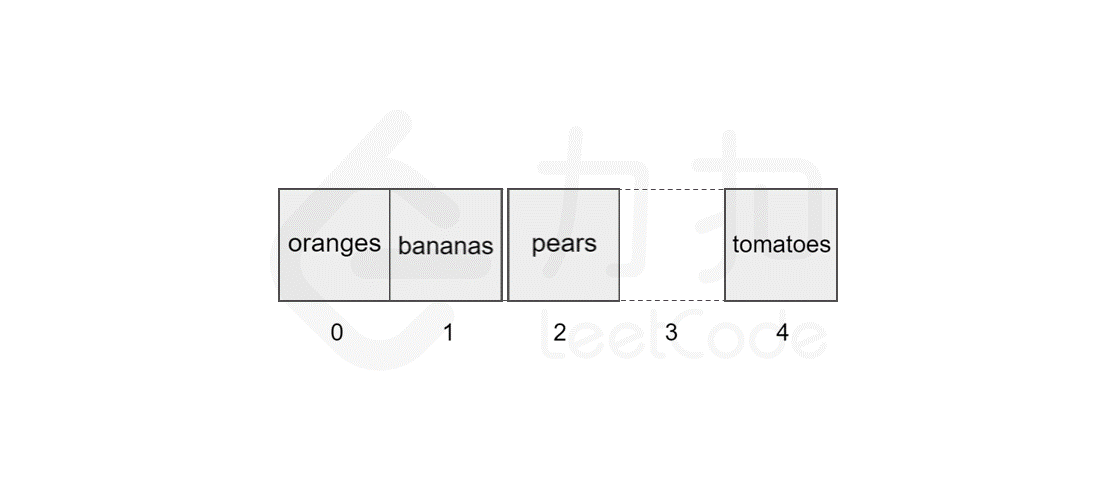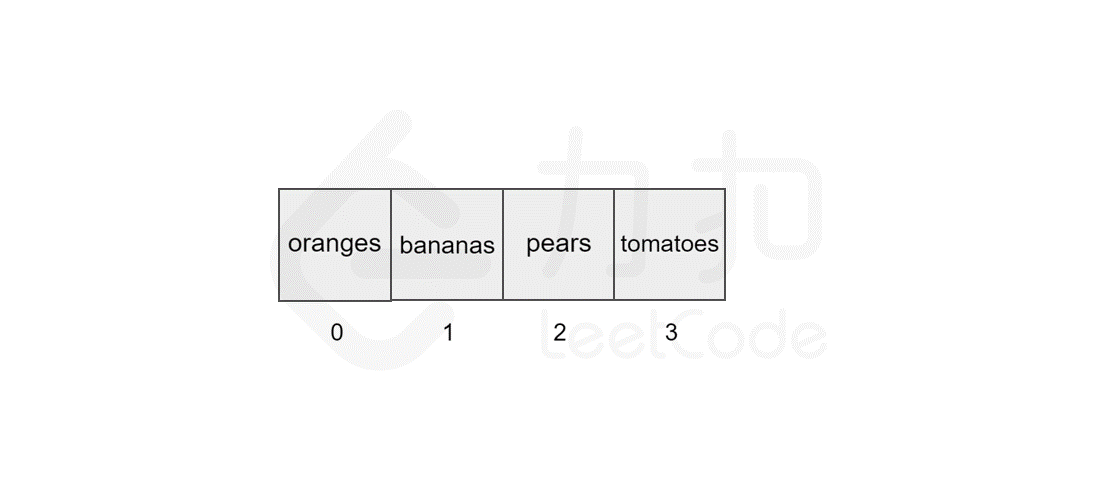 |
| 137 | + |
142 | 138 |
|
143 | 139 | 同样地,数组的长度为 `5`,最坏情况下,我们删除第一个元素,后面的 `4` 个元素需要向前移动,加上删除操作,共需执行 `5` 步,因此时间复杂度为 $O(N)$,*N* 为数组的长度。 |
144 | 140 |
|
|
150 | 146 |
|
151 | 147 | 二维数组是一种结构较为特殊的数组,只是将数组中的每个元素变成了一维数组。 |
152 | 148 |
|
153 | | -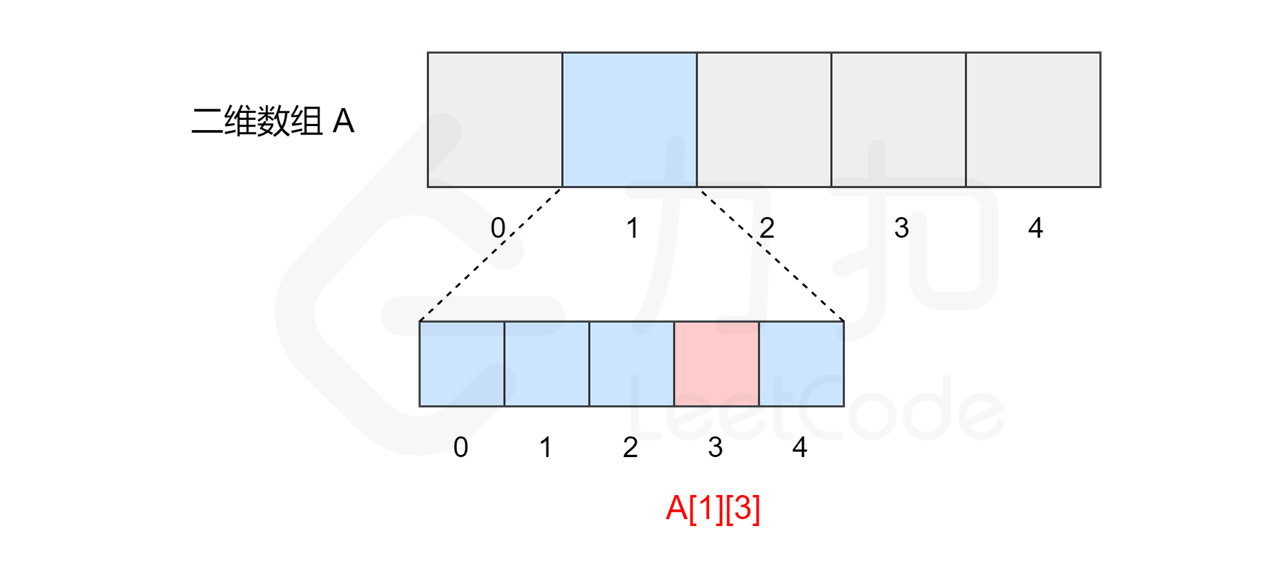 |
| 149 | + |
154 | 150 |
|
155 | 151 | 所以二维数组的本质上仍然是一个一维数组,内部的一维数组仍然从索引 `0` 开始,我们可以将它看作一个矩阵,并处理矩阵的相关问题。 |
156 | 152 |
|
|
160 | 156 |
|
161 | 157 | 类似一维数组,对于一个二维数组 `A = [[1, 2, 3, 4],[2, 4, 5, 6],[1, 4, 6, 8]]`,计算机同样会在内存中申请一段 **连续** 的空间,并记录第一行数组的索引位置,即 `A[0][0]` 的内存地址,它的索引与内存地址的关系如下图所示。 |
162 | 158 |
|
163 | | -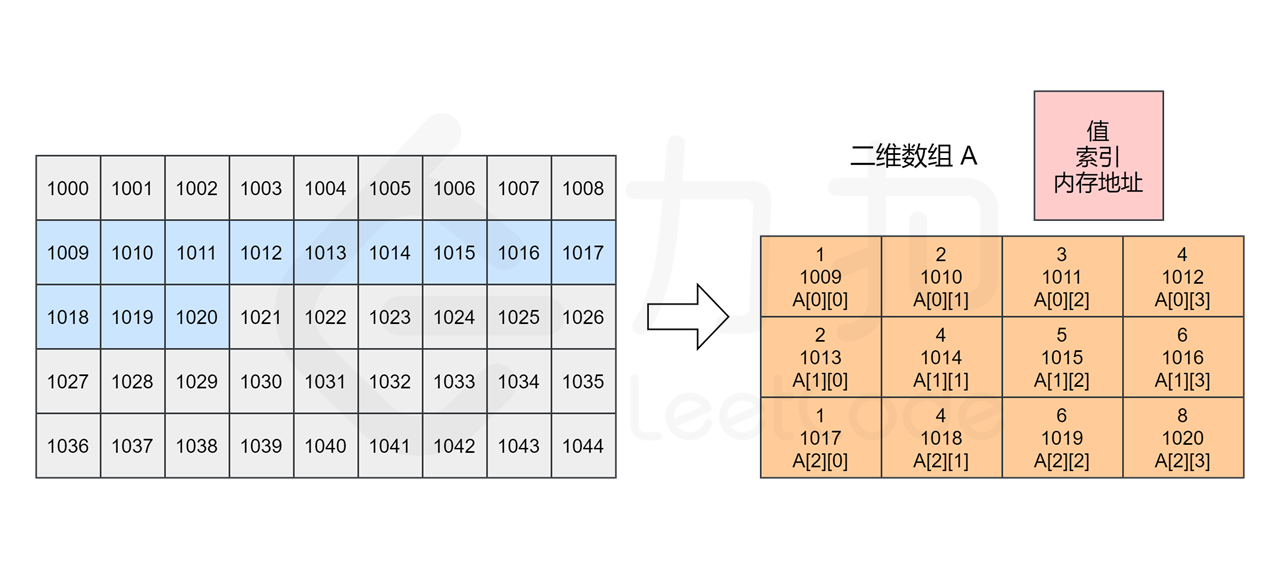 |
| 159 | + |
164 | 160 |
|
165 | 161 | 注意,实际数组中的元素由于类型的不同会占用不同的字节数,因此每个方格地址之间的差值可能不为 `1`。 |
166 | 162 |
|
|
0 commit comments